降维算法(Dimensionality Reduction Algorithm)

机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中 x 是原始数据点的表达，目前最多使用向量表达形式。 y 是数据点映射后的低维向量表达，通常 y 的维度小于 x 的维度（当然提高维度也是可以的）。f 可能是显式的或隐式的、线性的或非线性的。

目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据。之所以使用降维后的数据表示是因为在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用例如图像识别中造成了误差，降低了准确率；而通过降维, 我们希望减少冗余信息所造成的误差, 提高识别（或其他应用）的精度。又或者希望通过降维算法来寻找数据内部的本质结构特征。降维算法可以细分为特征选择和特征提取两大方法。

降维目前主要常用的降维算法是:主成分分析(PCA),线性判别分析(LDA),局部线性嵌入(LLE),拉普拉斯特征映射(LE)。

  • 主成分分析(Principal Component Analysis)

主成分分析(Principal Component Analysis,简称PCA)是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。

通俗的理解，如果把所有的点都映射到一起，那么几乎所有的信息（如点和点之间的距离关系）都丢失了，而如果映射后方差尽可能的大，那么数据点则会分散开来，以此来保留更多的信息。可以证明，PCA 是丢失原始数据信息最少的一种线性降维方式。（实际上就是最接近原始数据，但是 PCA 并不试图去探索数据内在结构）。

  • 线性判别分析(Linear Discriminant Analysis)

线性判别分析(Linear Discriminant Analysis,简称LDA)是一种有监督的（supervised）线性降维算法。与 PCA 保持数据信息不同，LDA 是为了使得降维后的数据点尽可能地容易被区分！

  • 局部线性嵌入(Locally Linear embedding)

局部线性嵌入(Locally Linear embedding,简称LLE）是一种非线性降维算法，它能够使降维后的数据较好地保持原有流形结构。LLE 可以说是流形学习方法最经典的工作之一。很多后续的流形学习、降维方法都与 LLE 有密切联系。

  • 拉普拉斯特征映射(Laplacian Eigenmaps)

拉普拉斯特征映射（Laplacian Eigenmaps,简称LE）看问题的角度和 LLE 有些相似，也是用局部的角度去构建数据之间的关系。它的直观思想是希望相互间有关系的点（在图中相连的点）在降维后的空间中尽可能的靠近。Laplacian Eigenmaps 可以反映出数据内在的流形结构。

降维算法(Dimensionality Reduction Algorithm)的应用算法有：

  • 主成分分析法(Principal Component Analysis)

  • 多维缩放(Mutiple Dimensional Scaling)

  • 线性判别分析(Linear Discriminant Analysis)

  • 等度量映射(IsometricMapping,Isomap)

  • 局部线性嵌入(Locally linear embedding)

  • 拉普拉斯特征映射(Laplacian Eigenmaps)

  • t－分布随机近邻嵌入(t-Distributed Stochastic Neighbor Embedding,t-SNE)

  • 深度自动编码器(Deep Autoencoder Networks)

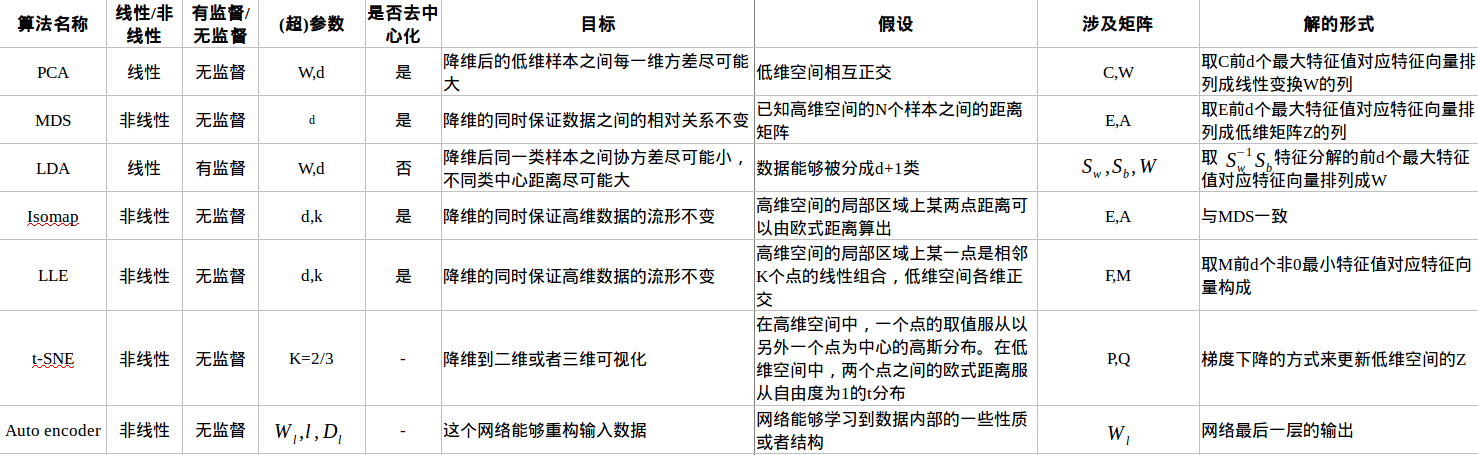
不同降维算法的区别和特征对比:

原文：https://github.com/KeKe-Li/tutorial