贝叶斯网络（Bayesian Belief Network）

贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，于1985年由Judea Pearl首先提出，它是基于概率推理的图形化网络，可以模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图。而贝叶斯公式则是这个概率网络的基础。贝叶斯网络是基于概率推理的数学模型，所谓概率推理就是通过一些变量的信息来获取其他的概率信息的过程，基于概率推理的贝叶斯网络(Bayesian network)是为了解决不定性和不完整性问题而提出的，它对于解决复杂设备不确定性和关联性引起的故障有很大的优势，在多个领域中获得广泛应用。

贝叶斯网络的有向无环图(Directed Acyclic Graph,DAG)中的节点表示随机变量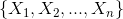，,由代表变量节点及连接这些节点有向边构成。它们可以是可观察到的变量，或隐变量、未知参数等。认为有因果关系（或非条件独立）的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。节点代表随机变量，节点间的有向边代表了节点间的互相关系(由父节点指向其子节点)，用条件概率进行表达关系强度，没有父节点的用先验概率进行信息表达。节点变量可以是任何问题的抽象，如：测试值，观测现象，意见征询等。适用于表达和分析不确定性和概率性的事件，应用于有条件地依赖多种控制因素的决策，可以从不完全、不精确或不确定的知识或信息中做出推理。

使用贝叶斯网络必须知道各个状态之间相关的概率。得到这些参数的过程叫做训练。和训练马尔可夫模型一样，训练贝叶斯网络要用一些已知的数据。比如在训练上面的网络，需要知道一些心血管疾病和吸烟、家族病史等有关的情况。相比马尔可夫链，贝叶斯网络的训练比较复杂，从理论上讲，它是一个 NP-complete问题，也就是说，现阶段没有可以在多项式时间内完成的算法。但是，对于某些应用，这个训练过程可以简化，并在计算上高效实现。

贝叶斯理论是处理不确定性信息的重要工具。作为一种基于概率的不确定性推理方法，贝叶斯网络在处理不确定信息的智能化系统中已得到了重要的应用，已成功地用于医疗诊断、统计决策、专家系统、学习预测等领域。这些成功的应用，充分体现了贝叶斯网络技术是一种强有力的不确定性推理方法。

应用示例

from bayesian.bbn import build_bbn

def f_prize_door(prize_door):
    return 0.33333333
def f_guest_door(guest_door):
    return 0.33333333
def f_monty_door(prize_door, guest_door, monty_door):
    if prize_door == guest_door:  # 参赛者猜对了
        if prize_door == monty_door:
            return 0     # Monty不会打开有车的那扇门，不可能发生
        else:
            return 0.5   # Monty会打开其它两扇门，二选一
    elif prize_door == monty_door:
        return 0         #  Monty不会打开有车的那扇门，不可能发生
    elif guest_door == monty_door:
        return 0         # 门已经由参赛者选定，不可能发生
    else:
        return 1    # Monty打开另一扇有羊的门

if __name__ == '__main__':
    g = build_bbn(
        f_prize_door,
        f_guest_door,
        f_monty_door,
        domains=dict(
            prize_door=['A', 'B', 'C'],
            guest_door=['A', 'B', 'C'],
            monty_door=['A', 'B', 'C']))

    g.q()
    g.q(guest_door='A')
g.q(guest_door='A', monty_door='B')

原文：https://github.com/KeKe-Li/tutorial