分类回归树
CART
CART:分类回归树(Classification And Regression Tree, CART)模型是决策树学习方法的一种，CART既可以用于分类计算，也可以用于回归。
CART本质是对特征空间进行二元划分（即CART生成的决策树是一棵二叉树），并能够对标量属性（nominal attribute）与连续属性（continuous attribute）进行分裂。
CART算法原理:CART决策树是结构简洁的二叉树，采用一种二分递归分割的技术，将当前的样本集分为两个子样本集，使得生成的每个非叶子的节点都有两个分支。与普通的决策树算法一样，CART算法包括两个过程：1）决策树的生成：基于训练数据集生成决策树，生成的决策树要尽量的大；2）决策树的剪枝：用验证数据集对以生成的树进行剪枝并选择最优子树，此时用损失函数最小作为剪枝的标准。
1.决策树的生成决策树的生成就是递归的构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼指数最小化原则，进行特征选择，生成二叉树。主要的原理如下：(1)分类树原理：分类树采用基尼指数（Gini index, Gini）选择最优特征，同时决定该特征的最优二值切分点。基尼指数定义为：
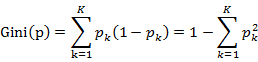
对于给定样本集合D，其基尼指数的计算为：
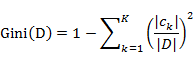
如果样本集合D根据特征A是否取某一可能值a被分割成D1和D2两部分，即：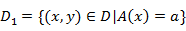
,D2=D-D1
则在特征A的条件下，集合D的基尼指数计算公式为：
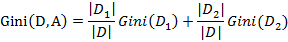
基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数值越大，样本集合的不确定性也就越大。
(2)回归树原理：回归树用平方误差最小化准则，进行特征选择，生成二叉树。将输入空间划分为M个区域R1，R2，…，Rm，则生成的回归树模型表示为：
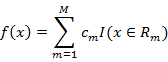
其中cm表示单元Rm上的最小误差平方的最优解.
2、决策树的剪枝
CART算法对于决策树剪枝方法，采用代价复杂度模型，通过交叉验证来估计对预测样本集的误分类损失，产生最小交叉验证误分类估计树。
CART剪枝算法主要由两步组成：首先从生成算法产生的决策树T0底端开始不断剪枝，直到T0的根节点，形成一个子树序列{T0，T1，… ，Tn}；然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树。
相关应用
分类回归树本质上也是一种决策树算法；而决策树分类器具有很好的准确性，已被成功的应用于许多的应用领域的分类，如医学、制造和生产、金融分析、天文学与分子生物学等；具体的包括欺诈监测、针对销售、性能预测、制造和医疗整段。决策树是许多商业规则归纳系统的基础。
优缺点
优点：可以生成易于理解的规则；计算量相对来说不大；可处理连续和离散字段；最终结果可清晰显示字段的重要性程度。缺点：对连续字段难以预测；处理时间序列数据，前期预处理步骤多；当类别太多，错误可能增加的较快。
wechat
alipay
