K-近邻算法（KNN）

K近邻算法是一种基于类比的分类方法，主要通过给定的检验组与和它相似的训练组进行比较来学习。训练组用n个属性来描述，每个元组代表n维空间上的点。当给定一个未知元组时，K最近邻分类法搜索该模式空间，找出最接近未知元组的k个训练组，并将未知元组指派到模式空间中它的k个最近邻中的多数类中。

k近邻（k-Nearest Neighbors）采用向量空间模型来分类，是一种常用的监督学习方法。它的工作原理为：给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个“邻居”的信息来进行预测。通常，在分类任务中可使用“投票法”，即选择这k个样本中出现最多的类别标记作为预测结果；在回归任务中可使用“平均法”，即将这k个样本的实值输出标记的平均值作为预测结果；还可基于距离远近进行加权平均或加权投票，距离越近的样本权重越大。

k近邻没有显式的训练过程，是“懒惰学习”的代表。此类学习技术在训练阶段仅仅是把样本保存起来，训练时间开销为零，待收到测试样本后再进行处理。

最近邻分类器虽然简单，但它的泛化错误率不超过贝叶斯最优分类器的错误率的两倍。

其中“最近邻”主要是以距离来度量的，一般使用欧几里得距离度量两个点或元组的距离，也可以使用曼哈顿距离或其他距离；欧几里得距离的主要计算公式如下：

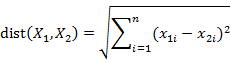
注意：为了防止具有较大初始值域的属性比较小初始值域的属性的权重过大，在计算距离之前，需对每个属性值进行规范化。一般的规划方法有最小-最大规范化，零均值规范化，小数定标规范化等。

最小-最大规范化：将原始数据值映射到[0,1]空间中，假定minA和maxA分别是属性A的最小值和最大值，则规范化的公式为：

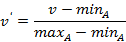
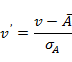
零均值规范化：基于属性A的均值和标准差上的规范化方法，具体计算如下：

小数定标规范化：通过移动属性A的小数点位置进行规范化，小数点的移动位数依赖于A的最大绝对值。具体计算如下：(其中j是使得MAX（ v’ ）<1的最小整数)

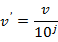
最近邻数K的确定，主要原理是选取产生最小误差率的k值。每次从k=1开始，使用检验集估计分类器的误差率；每次都允许增加一个近邻，重复该过程，选择误差率最小的k值。

应用案例


%matplotlib inline
import time
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_circles

N=210
K=2
MAX_ITERS = 1000
cut=int(N*0.7)

# 生成训练和测试数据集
data, features = make_circles(n_samples=N, shuffle=True, noise= 0.12, factor=0.4)
tr_data, tr_features= data[:cut], features[:cut]
te_data,te_features=data[cut:], features[cut:]

fig, ax = plt.subplots()
ax.scatter(tr_data.transpose()[0], tr_data.transpose()[1], marker = 'o', s = 100, c = tr_features, cmap=plt.cm.coolwarm )
ax.set_title('Train data')
plt.show()

start = time.time()

points=tf.Variable(data)
cluster_assignments = tf.Variable(tf.zeros([N], dtype=tf.int64))

sess = tf.Session()
sess.run(tf.initialize_all_variables())

te_learned_features=[]
for i, j in zip(te_data, te_features):
    distances = tf.reduce_sum(tf.square(tf.sub(i , tr_data)),reduction_indices=1)
    neighbor = tf.arg_min(distances,0)

    #print tr_features[sess.run(neighbor)]
    te_learned_features.append(tr_features[sess.run(neighbor)])

accuracy = tf.reduce_mean(tf.cast(tf.equal(te_learned_features, te_features), "float"))

fig, ax = plt.subplots()
ax.scatter(te_data.transpose()[0], te_data.transpose()[1], marker = 'o', s = 100, c = te_learned_features,       cmap=plt.cm.coolwarm )
ax.set_title('Test result')
plt.show()

end = time.time()
print ("Found in %.2f seconds" % (end-start))
print "Cluster assignments:", test
print "Accuracy:", sess.run(accuracy)

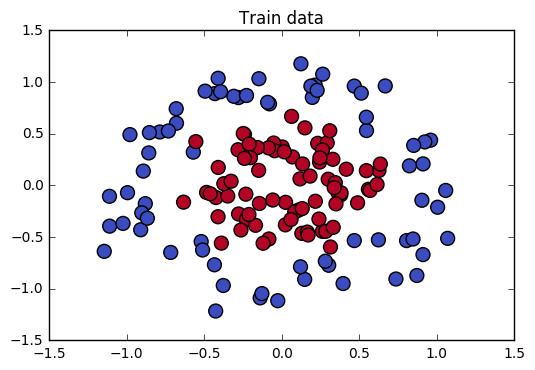
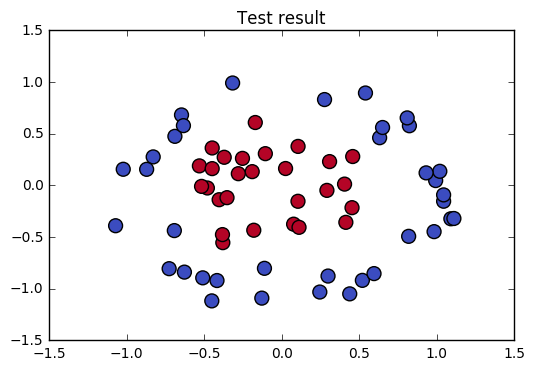
Found in 6.73 seconds
Cluster assignments: [0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0]
Accuracy: 1.0

原文：https://github.com/KeKe-Li/tutorial