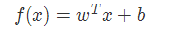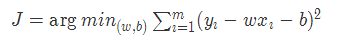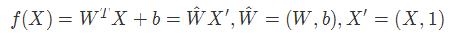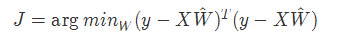%matplotlib inline
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
def model(X, w, b):
return tf.mul(w, X) + b
trX = np.mgrid[-1:1:0.01, -10:10:0.1].reshape(2, -1).T
trW = np.array([3, 5])
trY = trW*trX + np.random.randn(*trX.shape) + [20, 100]
w = tf.Variable(np.array([1., 1.]).astype(np.float32))
b = tf.Variable(np.array([[1., 1.]]).astype(np.float32))
cost = tf.reduce_mean(tf.square(trY-model(trX, w, b)))
train_op = tf.train.GradientDescentOptimizer(0.05).minimize(cost)
with tf.Session() as sess:
tf.initialize_all_variables().run()
for i in range(1000):
if i % 99 == 0:
print "Cost at step", i, "is:", cost.eval()
sess.run(train_op)
print "w should be something around [3, 5]: ", sess.run(w)
print "b should be something around [20,100]:", sess.run(b)
Cost at step 0 is: 5329.87
Cost at step 99 is: 1.22204
Cost at step 198 is: 0.998043
Cost at step 297 is: 0.997083
Cost at step 396 is: 0.997049
Cost at step 495 is: 0.997049
Cost at step 594 is: 0.997049
Cost at step 693 is: 0.997049
Cost at step 792 is: 0.997049
Cost at step 891 is: 0.997049
Cost at step 990 is: 0.997049
w should be something around [3, 5]: [ 3.00108743 5.00054932]
b should be something around [20,100]: [[ 20.00317383 100.00382233]]
tensorflow示例
import tensorflow as tf
W = tf.Variable(tf.zeros([2, 1]), name="weights")
b = tf.Variable(0., name="bias")
def inference(X):
return tf.matmul(X, W) + b
def loss(X, Y):
Y_predicted = inference(X)
return tf.reduce_sum(tf.squared_difference(Y, Y_predicted))
def inputs():
weight_age = [[84, 46], [73, 20], [65, 52], [70, 30], [76, 57], [69, 25], [63, 28], [72, 36], [79, 57], [75, 44], [27, 24], [89, 31], [65, 52], [57, 23], [59, 60], [69, 48], [60, 34], [79, 51], [75, 50], [82, 34], [59, 46], [67, 23], [85, 37], [55, 40], [63, 30]]
blood_fat_content = [354, 190, 405, 263, 451, 302, 288, 385, 402, 365, 209, 290, 346, 254, 395, 434, 220, 374, 308, 220, 311, 181, 274, 303, 244]
return tf.to_float(weight_age), tf.to_float(blood_fat_content)
def train(total_loss):
learning_rate = 0.000001
return tf.train.GradientDescentOptimizer(learning_rate).minimize(total_loss)
def evaluate(sess, X, Y):
print sess.run(inference([[80., 25.]]))
print sess.run(inference([[65., 25.]]))
with tf.Session() as sess:
tf.initialize_all_variables().run()
X, Y = inputs()
total_loss = loss(X, Y)
train_op = train(total_loss)
coord = tf.train.Coordinator()
threads = tf.train.start_queue_runners(sess=sess, coord=coord)
training_steps = 1000
for step in range(training_steps):
sess.run([train_op])
if step % 10 == 0:
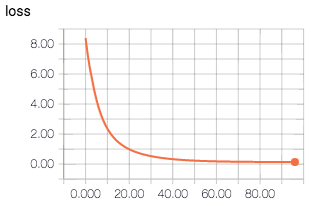
print "loss at step ", step, ":", sess.run([total_loss])
evaluate(sess, X, Y)
coord.request_stop()
coord.join(threads)
|