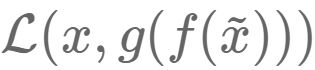import struct
import array
import numpy
import math
import time
import scipy.io
import scipy.optimize
""" Returns elementwise sigmoid output of input array """
def sigmoid(x):
return (1 / (1 + numpy.exp(-x)))
""" Returns the groundtruth matrix for a set of labels """
def getGroundTruth(labels):
""" Prepare data needed to construct groundtruth matrix """
labels = numpy.array(labels).flatten()
data = numpy.ones(len(labels))
indptr = numpy.arange(len(labels)+1)
""" Compute the groundtruth matrix and return """
ground_truth = scipy.sparse.csr_matrix((data, labels, indptr))
ground_truth = numpy.transpose(ground_truth.todense())
return ground_truth
""" The Sparse Autoencoder class """
class SparseAutoencoder(object):
""" Initialization of Autoencoder object """
def __init__(self, visible_size, hidden_size, rho, lamda, beta):
""" Initialize parameters of the Autoencoder object """
self.visible_size = visible_size
self.hidden_size = hidden_size
self.rho = rho
self.lamda = lamda
self.beta = beta
""" Set limits for accessing 'theta' values """
self.limit0 = 0
self.limit1 = hidden_size * visible_size
self.limit2 = 2 * hidden_size * visible_size
self.limit3 = 2 * hidden_size * visible_size + hidden_size
self.limit4 = 2 * hidden_size * visible_size + hidden_size + visible_size
""" Initialize Neural Network weights randomly
W1, W2 values are chosen in the range [-r, r] """
r = math.sqrt(6) / math.sqrt(visible_size + hidden_size + 1)
rand = numpy.random.RandomState(int(time.time()))
W1 = numpy.asarray(rand.uniform(low = -r, high = r, size = (hidden_size, visible_size)))
W2 = numpy.asarray(rand.uniform(low = -r, high = r, size = (visible_size, hidden_size)))
""" Bias values are initialized to zero """
b1 = numpy.zeros((hidden_size, 1))
b2 = numpy.zeros((visible_size, 1))
""" Create 'theta' by unrolling W1, W2, b1, b2 """
self.theta = numpy.concatenate((W1.flatten(), W2.flatten(),
b1.flatten(), b2.flatten()))
""" Returns gradient of 'theta' using Backpropagation algorithm """
def sparseAutoencoderCost(self, theta, input):
""" Extract weights and biases from 'theta' input """
W1 = theta[self.limit0 : self.limit1].reshape(self.hidden_size, self.visible_size)
W2 = theta[self.limit1 : self.limit2].reshape(self.visible_size, self.hidden_size)
b1 = theta[self.limit2 : self.limit3].reshape(self.hidden_size, 1)
b2 = theta[self.limit3 : self.limit4].reshape(self.visible_size, 1)
""" Compute output layers by performing a feedforward pass
Computation is done for all the training inputs simultaneously """
hidden_layer = sigmoid(numpy.dot(W1, input) + b1)
output_layer = sigmoid(numpy.dot(W2, hidden_layer) + b2)
""" Estimate the average activation value of the hidden layers """
rho_cap = numpy.sum(hidden_layer, axis = 1) / input.shape[1]
""" Compute intermediate difference values using Backpropagation algorithm """
diff = output_layer - input
sum_of_squares_error = 0.5 * numpy.sum(numpy.multiply(diff, diff)) / input.shape[1]
weight_decay = 0.5 * self.lamda * (numpy.sum(numpy.multiply(W1, W1)) +
numpy.sum(numpy.multiply(W2, W2)))
KL_divergence = self.beta * numpy.sum(self.rho * numpy.log(self.rho / rho_cap) +
(1 - self.rho) * numpy.log((1 - self.rho) / (1 - rho_cap)))
cost = sum_of_squares_error + weight_decay + KL_divergence
KL_div_grad = self.beta * (-(self.rho / rho_cap) + ((1 - self.rho) / (1 - rho_cap)))
del_out = numpy.multiply(diff, numpy.multiply(output_layer, 1 - output_layer))
del_hid = numpy.multiply(numpy.dot(numpy.transpose(W2), del_out) + numpy.transpose(numpy.matrix(KL_div_grad)),
numpy.multiply(hidden_layer, 1 - hidden_layer))
""" Compute the gradient values by averaging partial derivatives
Partial derivatives are averaged over all training examples """
W1_grad = numpy.dot(del_hid, numpy.transpose(input))
W2_grad = numpy.dot(del_out, numpy.transpose(hidden_layer))
b1_grad = numpy.sum(del_hid, axis = 1)
b2_grad = numpy.sum(del_out, axis = 1)
W1_grad = W1_grad / input.shape[1] + self.lamda * W1
W2_grad = W2_grad / input.shape[1] + self.lamda * W2
b1_grad = b1_grad / input.shape[1]
b2_grad = b2_grad / input.shape[1]
""" Transform numpy matrices into arrays """
W1_grad = numpy.array(W1_grad)
W2_grad = numpy.array(W2_grad)
b1_grad = numpy.array(b1_grad)
b2_grad = numpy.array(b2_grad)
""" Unroll the gradient values and return as 'theta' gradient """
theta_grad = numpy.concatenate((W1_grad.flatten(), W2_grad.flatten(),
b1_grad.flatten(), b2_grad.flatten()))
return [cost, theta_grad]
""" The Softmax Regression class """
class SoftmaxRegression(object):
""" Initialization of Regressor object """
def __init__(self, input_size, num_classes, lamda):
""" Initialize parameters of the Regressor object """
self.input_size = input_size
self.num_classes = num_classes
self.lamda = lamda
""" Randomly initialize the class weights """
rand = numpy.random.RandomState(int(time.time()))
self.theta = 0.005 * numpy.asarray(rand.normal(size = (num_classes*input_size, 1)))
""" Returns the cost and gradient of 'theta' at a particular 'theta' """
def softmaxCost(self, theta, input, labels):
""" Compute the groundtruth matrix """
ground_truth = getGroundTruth(labels)
""" Reshape 'theta' for ease of computation """
theta = theta.reshape(self.num_classes, self.input_size)
""" Compute the class probabilities for each example """
theta_x = numpy.dot(theta, input)
hypothesis = numpy.exp(theta_x)
probabilities = hypothesis / numpy.sum(hypothesis, axis = 0)
""" Compute the traditional cost term """
cost_examples = numpy.multiply(ground_truth, numpy.log(probabilities))
traditional_cost = -(numpy.sum(cost_examples) / input.shape[1])
""" Compute the weight decay term """
theta_squared = numpy.multiply(theta, theta)
weight_decay = 0.5 * self.lamda * numpy.sum(theta_squared)
""" Add both terms to get the cost """
cost = traditional_cost + weight_decay
""" Compute and unroll 'theta' gradient """
theta_grad = -numpy.dot(ground_truth - probabilities, numpy.transpose(input))
theta_grad = theta_grad / input.shape[1] + self.lamda * theta
theta_grad = numpy.array(theta_grad)
theta_grad = theta_grad.flatten()
return [cost, theta_grad]
""" Loads the images from the provided file name """
def loadMNISTImages(file_name):
""" Open the file """
image_file = open(file_name, 'rb')
""" Read header information from the file """
head1 = image_file.read(4)
head2 = image_file.read(4)
head3 = image_file.read(4)
head4 = image_file.read(4)
""" Format the header information for useful data """
num_examples = struct.unpack('>I', head2)[0]
num_rows = struct.unpack('>I', head3)[0]
num_cols = struct.unpack('>I', head4)[0]
""" Initialize dataset as array of zeros """
dataset = numpy.zeros((num_rows*num_cols, num_examples))
""" Read the actual image data """
images_raw = array.array('B', image_file.read())
image_file.close()
""" Arrange the data in columns """
for i in range(num_examples):
limit1 = num_rows * num_cols * i
limit2 = num_rows * num_cols * (i + 1)
dataset[:, i] = images_raw[limit1 : limit2]
""" Normalize and return the dataset """
return dataset / 255
""" Loads the image labels from the provided file name """
def loadMNISTLabels(file_name):
""" Open the file """
label_file = open(file_name, 'rb')
""" Read header information from the file """
head1 = label_file.read(4)
head2 = label_file.read(4)
""" Format the header information for useful data """
num_examples = struct.unpack('>I', head2)[0]
""" Initialize data labels as array of zeros """
labels = numpy.zeros((num_examples, 1), dtype = numpy.int)
""" Read the label data """
labels_raw = array.array('b', label_file.read())
label_file.close()
""" Copy and return the label data """
labels[:, 0] = labels_raw[:]
return labels
""" Returns the hidden layer activations of the Autoencoder """
def feedForwardAutoencoder(theta, hidden_size, visible_size, input):
""" Define limits to access useful data """
limit0 = 0
limit1 = hidden_size * visible_size
limit2 = 2 * hidden_size * visible_size
limit3 = 2 * hidden_size * visible_size + hidden_size
""" Access W1 and b1 from 'theta' """
W1 = theta[limit0 : limit1].reshape(hidden_size, visible_size)
b1 = theta[limit2 : limit3].reshape(hidden_size, 1)
""" Compute the hidden layer activations """
hidden_layer = 1 / (1 + numpy.exp(-(numpy.dot(W1, input) + b1)))
return hidden_layer
""" Returns a row of Stacked Autoencoder parameters """
def stack2Params(stack):
""" Initialize an empty list of parameters """
params = []
num_layers = len(stack) / 2
""" For each layer in the neural network, append the corresponding parameters """
for i in range(num_layers):
params = numpy.concatenate((params, numpy.array(stack[i, "W"]).flatten()))
params = numpy.concatenate((params, numpy.array(stack[i, "b"]).flatten()))
return params
""" Returns a stack of Stacked Autoencoder parameters """
def params2Stack(params, net_config):
""" Initialize an empty stack """
stack = {}
limit0 = 0
for i in range(len(net_config)-2):
""" Calculate limits of layer parameters, using neural network config """
limit1 = limit0 + net_config[i] * net_config[i+1]
limit2 = limit1 + net_config[i+1]
""" Extract layer parameters, and store in the stack """
stack[i, "W"] = params[limit0 : limit1].reshape(net_config[i+1], net_config[i])
stack[i, "b"] = params[limit1 : limit2].reshape(net_config[i+1], 1)
limit0 = limit2
return stack
""" Function for finetuning the Stacked Autoencoder """
def stackedAutoencoderCost(theta, net_config, lamda, data, labels):
""" Calculate limits for Softmax parameters """
input_size = net_config[-2]
num_classes = net_config[-1]
limit0 = 0
limit1 = num_classes * input_size
""" Extract Softmax and layer parameters """
softmax_theta = theta[limit0 : limit1].reshape(num_classes, input_size)
stack = params2Stack(theta[limit1 :], net_config)
num_layers = len(stack) / 2
""" Calculate activations for every layer """
activation = {}
activation[0] = data
for i in range(num_layers):
activation[i+1] = sigmoid(numpy.dot(stack[i, "W"], activation[i]) + stack[i, "b"])
""" Compute the groundtruth matrix """
ground_truth = getGroundTruth(labels)
""" Compute the class probabilities for each example """
theta_x = numpy.dot(softmax_theta, activation[num_layers])
hypothesis = numpy.exp(theta_x)
probabilities = hypothesis / numpy.sum(hypothesis, axis = 0)
""" Compute the traditional cost term """
cost_examples = numpy.multiply(ground_truth, numpy.log(probabilities))
traditional_cost = -(numpy.sum(cost_examples) / data.shape[1])
""" Compute the weight decay term """
theta_squared = numpy.multiply(softmax_theta, softmax_theta)
weight_decay = 0.5 * lamda * numpy.sum(theta_squared)
""" Add both terms to get the cost """
cost = traditional_cost + weight_decay
""" Compute Softmax 'theta' gradient """
softmax_theta_grad = -numpy.dot(ground_truth - probabilities, numpy.transpose(activation[num_layers]))
softmax_theta_grad = softmax_theta_grad / data.shape[1] + lamda * softmax_theta
""" Compute intermediate difference values using Backpropagation algorithm """
delta = {}
delta[num_layers] = -numpy.multiply(numpy.dot(numpy.transpose(softmax_theta), ground_truth - probabilities),
numpy.multiply(activation[num_layers], 1 - activation[num_layers]))
for i in range(num_layers-1):
index = num_layers - i - 1
delta[index] = numpy.multiply(numpy.dot(numpy.transpose(stack[index, "W"]), delta[index+1]),
numpy.multiply(activation[index], 1 - activation[index]))
""" Compute the partial derivatives, with respect to the layer parameters """
stack_grad = {}
for i in range(num_layers):
index = num_layers - i - 1
stack_grad[index, "W"] = numpy.dot(delta[index+1], numpy.transpose(activation[index])) / data.shape[1]
stack_grad[index, "b"] = numpy.sum(delta[index+1], axis = 1) / data.shape[1]
""" Concatenate the gradient values and return as 'theta' gradient """
params_grad = stack2Params(stack_grad)
theta_grad = numpy.concatenate((numpy.array(softmax_theta_grad).flatten(),
numpy.array(params_grad).flatten()))
return [cost, theta_grad]
""" Returns predictions using the trained Stacked Autoencoder model """
def stackedAutoencoderPredict(theta, net_config, data):
""" Calculate limits for Softmax parameters """
input_size = net_config[-2]
num_classes = net_config[-1]
limit0 = 0
limit1 = num_classes * input_size
""" Extract Softmax and layer parameters """
softmax_theta = theta[limit0 : limit1].reshape(num_classes, input_size)
stack = params2Stack(theta[limit1 :], net_config)
num_layers = len(stack) / 2
""" Calculate the activations of the final layer """
activation = data
for i in range(num_layers):
activation = sigmoid(numpy.dot(stack[i, "W"], activation) + stack[i, "b"])
""" Compute the class probabilities for each example """
theta_x = numpy.dot(softmax_theta, activation)
hypothesis = numpy.exp(theta_x)
probabilities = hypothesis / numpy.sum(hypothesis, axis = 0)
""" Give the predictions based on probability values """
predictions = numpy.zeros((data.shape[1], 1))
predictions[:, 0] = numpy.argmax(probabilities, axis = 0)
return predictions
""" Loads data, trains the Stacked Autoencoder model and predicts classes for test data """
def executeStackedAutoencoder():
""" Define the parameters of the first Autoencoder """
visible_size = 784
hidden_size1 = 200
hidden_size2 = 200
rho = 0.1
lamda = 0.003
beta = 3
max_iterations = 200
num_classes = 10
""" Load MNIST images for training and testing """
train_data = loadMNISTImages('train-images.idx3-ubyte')
train_labels = loadMNISTLabels('train-labels.idx1-ubyte')
""" Initialize the first Autoencoder with the above parameters """
encoder1 = SparseAutoencoder(visible_size, hidden_size1, rho, lamda, beta)
""" Run the L-BFGS algorithm to get the optimal parameter values """
opt_solution = scipy.optimize.minimize(encoder1.sparseAutoencoderCost, encoder1.theta,
args = (train_data,), method = 'L-BFGS-B',
jac = True, options = {'maxiter': max_iterations})
sae1_opt_theta = opt_solution.x
""" Get the features corresponding to first Autoencoder """
sae1_features = feedForwardAutoencoder(sae1_opt_theta, hidden_size1, visible_size, train_data)
""" Initialize the second Autoencoder with the above parameters """
encoder2 = SparseAutoencoder(hidden_size1, hidden_size2, rho, lamda, beta)
""" Run the L-BFGS algorithm to get the optimal parameter values """
opt_solution = scipy.optimize.minimize(encoder2.sparseAutoencoderCost, encoder2.theta,
args = (sae1_features,), method = 'L-BFGS-B',
jac = True, options = {'maxiter': max_iterations})
sae2_opt_theta = opt_solution.x
""" Get the features corresponding to second Autoencoder """
sae2_features = feedForwardAutoencoder(sae2_opt_theta, hidden_size2, hidden_size1, sae1_features)
""" Initialize Softmax Regressor with the above parameters """
regressor = SoftmaxRegression(hidden_size2, num_classes, lamda)
""" Run the L-BFGS algorithm to get the optimal parameter values """
opt_solution = scipy.optimize.minimize(regressor.softmaxCost, regressor.theta,
args = (sae2_features, train_labels,), method = 'L-BFGS-B',
jac = True, options = {'maxiter': max_iterations})
softmax_opt_theta = opt_solution.x
""" Create a stack of the Stacked Autoencoder parameters """
stack = {}
stack[0, "W"] = sae1_opt_theta[encoder1.limit0 : encoder1.limit1].reshape(hidden_size1, visible_size)
stack[1, "W"] = sae2_opt_theta[encoder2.limit0 : encoder2.limit1].reshape(hidden_size2, hidden_size1)
stack[0, "b"] = sae1_opt_theta[encoder1.limit2 : encoder1.limit3].reshape(hidden_size1, 1)
stack[1, "b"] = sae2_opt_theta[encoder2.limit2 : encoder2.limit3].reshape(hidden_size2, 1)
""" Create a vector of the Stacked Autoencoder parameters for optimization """
stack_params = stack2Params(stack)
stacked_ae_theta = numpy.concatenate((softmax_opt_theta.flatten(), stack_params.flatten()))
""" Create a neural network configuration, with number of units in each layer """
net_config = [visible_size, hidden_size1, hidden_size2, num_classes]
""" Load MNIST test images and labels """
test_data = loadMNISTImages('t10k-images.idx3-ubyte')
test_labels = loadMNISTLabels('t10k-labels.idx1-ubyte')
""" Get predictions after greedy training """
predictions = stackedAutoencoderPredict(stacked_ae_theta, net_config, test_data)
""" Print accuracy of the trained model """
correct = test_labels[:, 0] == predictions[:, 0]
print """Accuracy after greedy training :""", numpy.mean(correct)
""" Finetune the greedily trained model """
opt_solution = scipy.optimize.minimize(stackedAutoencoderCost, stacked_ae_theta,
args = (net_config, lamda, train_data, train_labels,),
method = 'L-BFGS-B', jac = True, options = {'maxiter': max_iterations})
stacked_ae_opt_theta = opt_solution.x
""" Get predictions after finetuning """
predictions = stackedAutoencoderPredict(stacked_ae_opt_theta, net_config, test_data)
""" Print accuracy of the trained model """
correct = test_labels[:, 0] == predictions[:, 0]
print """Accuracy after finetuning :""", numpy.mean(correct)
executeStackedAutoencoder()
|
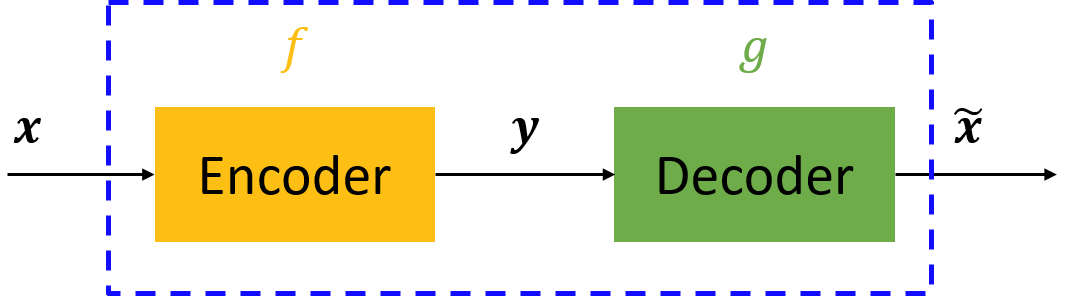
![]() ,即
,即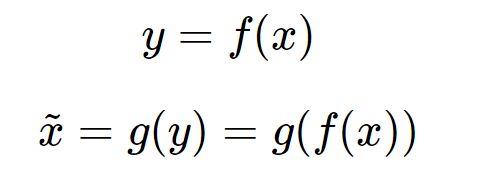
 ,实际上事实确实如此,但这样的变换就没有什么用了,所以我们需要对中间信号y(也叫作“编码”)做一定的约束,这样,系统往往能学出很有趣的编码变换f和编码y。
,实际上事实确实如此,但这样的变换就没有什么用了,所以我们需要对中间信号y(也叫作“编码”)做一定的约束,这样,系统往往能学出很有趣的编码变换f和编码y。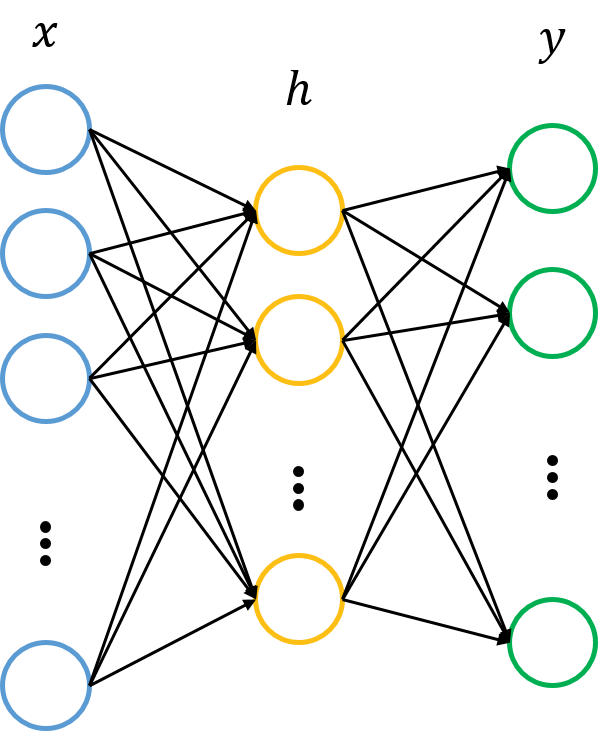
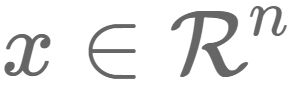 转换到中间层(隐层)
转换到中间层(隐层)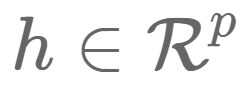 ,再转换到输出层
,再转换到输出层 。图中的每个节点代表数据的一个维度(偏置项图中未标出)。每两层之间的变换都是“线性变化”+“非线性激活”,用公式表示即为。图中的每个节点代表数据的一个维度(偏置项图中未标出)。每两层之间的变换都是“线性变化”+“非线性激活”,用公式表示为:
。图中的每个节点代表数据的一个维度(偏置项图中未标出)。每两层之间的变换都是“线性变化”+“非线性激活”,用公式表示即为。图中的每个节点代表数据的一个维度(偏置项图中未标出)。每两层之间的变换都是“线性变化”+“非线性激活”,用公式表示为: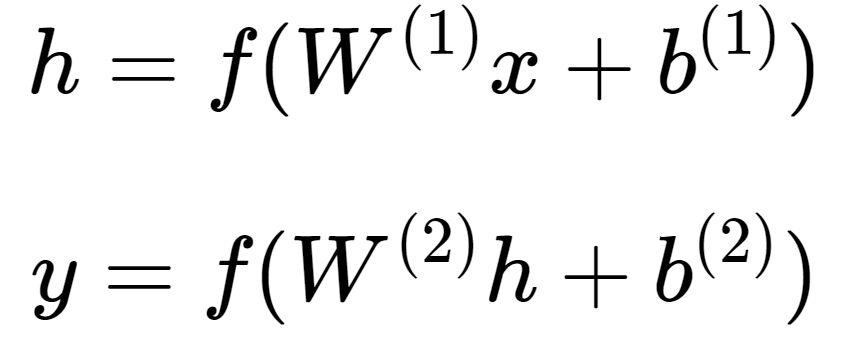
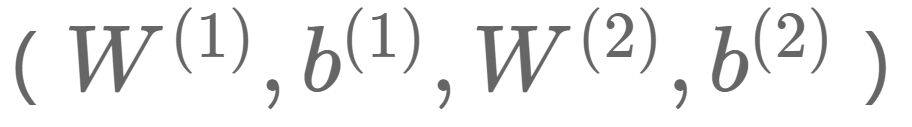 ,以使得整个网络尽可能去拟合训练数据。如果有正则约束的话,还同时要求模型尽量简单(以防止过拟合)。
,以使得整个网络尽可能去拟合训练数据。如果有正则约束的话,还同时要求模型尽量简单(以防止过拟合)。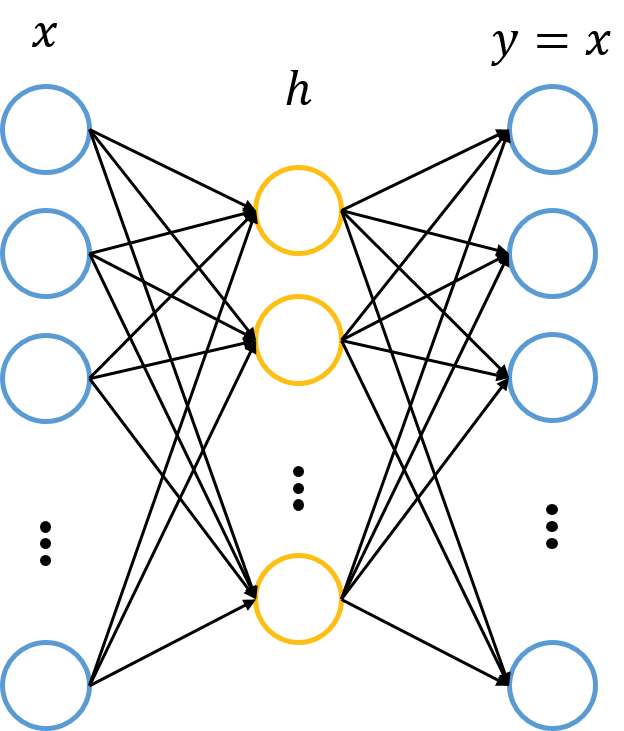
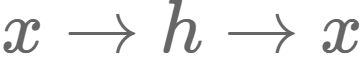 的能力。对我们来说,此时的h是至关重要的,因为它是在尽量不损失信息量的情况下,对原始数据的另一种表达。结合神经网络的惯例,我们再将自编码器的公式表示如下:(假设激活函数是sigmoid,用s表示)
的能力。对我们来说,此时的h是至关重要的,因为它是在尽量不损失信息量的情况下,对原始数据的另一种表达。结合神经网络的惯例,我们再将自编码器的公式表示如下:(假设激活函数是sigmoid,用s表示)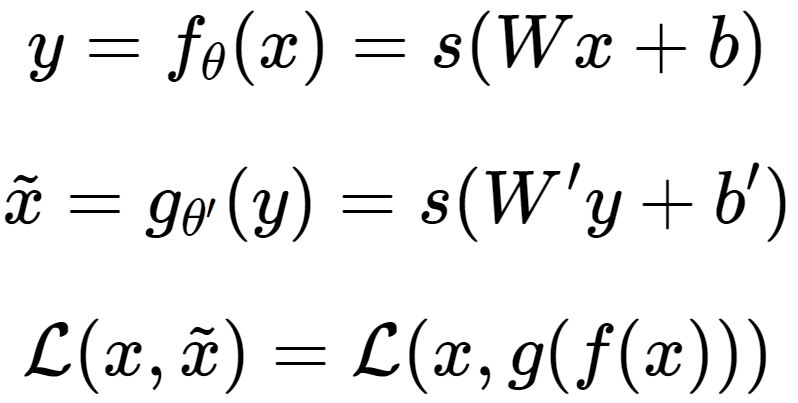
![]() 表示损失函数,结合数据的不同形式,可以是二次误差(squared error loss)或交叉熵误差(cross entropy loss)。如果
表示损失函数,结合数据的不同形式,可以是二次误差(squared error loss)或交叉熵误差(cross entropy loss)。如果![]() ,一般称为tied weights。
,一般称为tied weights。![]() 的三层网络,能够学习出一种特征变化
的三层网络,能够学习出一种特征变化![]() (这里用θ表示变换的参数,包括W,b和激活函数)。实际上,当训练结束后,输出层就没什么意义了,我们一般会将其去掉的,即将自编码器表示为:
(这里用θ表示变换的参数,包括W,b和激活函数)。实际上,当训练结束后,输出层就没什么意义了,我们一般会将其去掉的,即将自编码器表示为:

![]() 与期望激活度ρ之间的差异即可,然后将这个度量添加到目标函数作为正则,训练整个网络即可。那么,什么样的度量适合这个任务呢?了解过概率论、信息论基础的人应该清楚——相对熵,也就是KL散度(KL divergence)。因此,整个网络所添加的惩罚项:
与期望激活度ρ之间的差异即可,然后将这个度量添加到目标函数作为正则,训练整个网络即可。那么,什么样的度量适合这个任务呢?了解过概率论、信息论基础的人应该清楚——相对熵,也就是KL散度(KL divergence)。因此,整个网络所添加的惩罚项: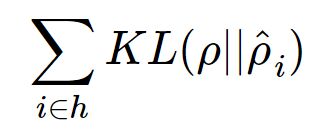
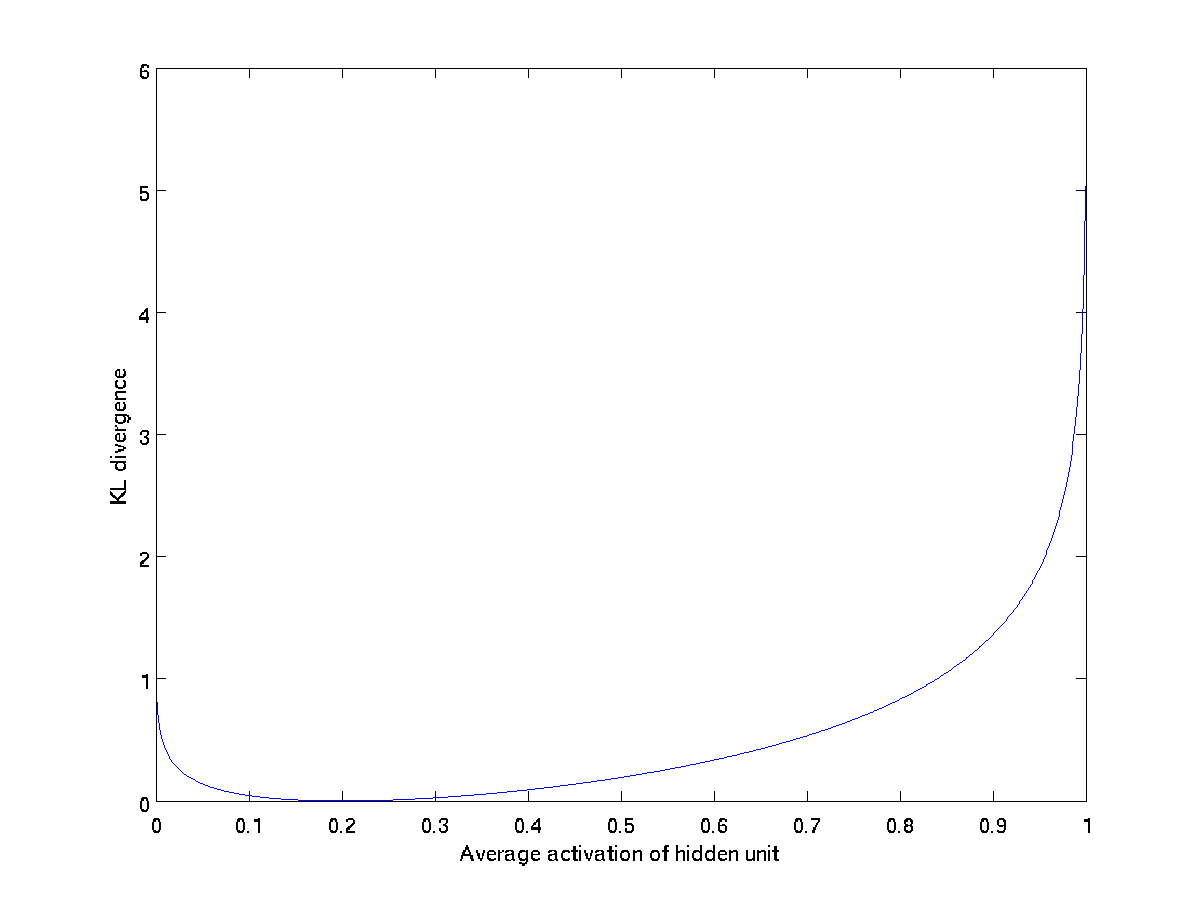
![]() 一旦偏离期望激活度ρ,这种误差便急剧增大,从而作为惩罚项添加到目标函数,指导整个网络学习出稀疏的特征表达。
一旦偏离期望激活度ρ,这种误差便急剧增大,从而作为惩罚项添加到目标函数,指导整个网络学习出稀疏的特征表达。![]() ,然后再对
,然后再对![]() 编码、解码,得到恢复信号
编码、解码,得到恢复信号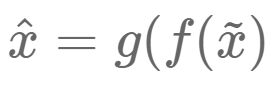 ,该恢复信号尽可能逼近未被污染的数据x。此时,监督训练的误差从
,该恢复信号尽可能逼近未被污染的数据x。此时,监督训练的误差从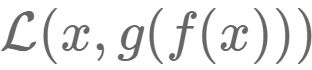 变成了
变成了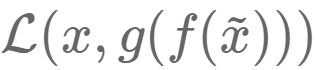 。
。